Bizzo Casino is a cutting-edge mobile-friendly casino that invites new players to enjoy a distinctive gaming experience. Tournaments, a fantastic bonus scheme, and top suppliers are just a few of…
A Step-By-Step Guide to Getting Started With IviBet
So you want to start gambling—now what? Well, the good news is that you have come to the right place. The even better news is that all you need is…
GUIDE TO INTUITIVE WAY OF EATING
We all know good resolutions when it comes to nutrition. Instead of forbidding yourself certain foods, maybe you’d rather learn to enjoy them to reach your ideal weight. This works…
Why is 22Bet Casino the best resort for you?
22 Bet Casino – it’s still relatively unknown right now, but many gamers instantly rated this online casino as a resort to help them out. The bookmakers have established a…
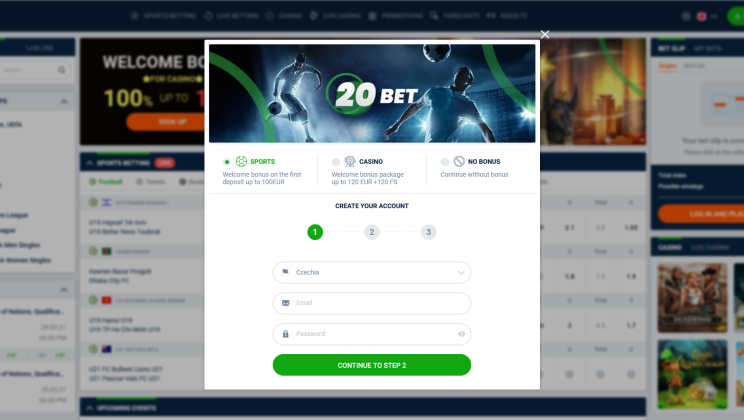
Have You Seen The Perfect Casino Website: Bet20 Calls For New Winners
Regardless of the fact that Bet20 only began providing Internet sports betting and wagering in 2020, this internet platform has swiftly achieved significant awareness. At first look, Bet20 Casino appears…
22Bet: Numerous deposit and withdrawal options, generous bonuses, and responsive customer support.
22Bet is the best choice for Italian gamers and bettors. Sports markets and betting options abound, with hundreds of sporting events available each day, and a wide variety of options…
Beauty and the Beast Slot Machine
Introducing Beauty and the Beast Slot Machine, a beautiful casino game inspired by the fairy tale Beauty and the Beast. Many of us know this story that our grandmothers told…
Faerie Spells Slot Machine
It is in a forest, that the slot machine presents itself. Hidden from human eyes, between the leaves of the trees, is where the world of fairies hides. In the…
WHAT FACTORS INFLUENCE TEAMS IN RETURN MATCHES?
In essence and principle, betting on return games is not much different from those in the regular championships. The same favourites, similarly there can be underdogs and strong midfielders. However,…
Popular betting – with the crowd along the way or better against the current?
Crowd Opinions/Investments – Features Of Betting Behind The Majority The main aim of betting shops is to balance the flow of customer money. To do this, the betting shops change…










Recent Comments